Többállapotú SEIR modell szimulátor | Koronavírus információs oldal

1,18

Tetőzés időpontja

ismeretlen

Fertőzésen átesettek undefined nap alatt

NaN%

Alapvető paraméterek

Időtáv:

Logaritmikus skála

0,17

0,0% / hét

4,9%

12,5%

47%

Betegség lefolyásának paraméterei

5,1 nap

6,9 nap

6,5 nap

6,1 nap

Kezdeti feltételek

Lappangók

2 598

Fertőzőek

5 196

Halálozások

30 098

A modell leírása

Az itt látható modell a klasszikus SEIR (susceptible-exposed-infected-removed) modell néhány további kompartmenttel kiegészített változata. A modellben a teljes lakosságot az alábbi kategóriákba soroljuk (minden ember egyszerre csak egy kategóriába tartozhat):

Még nem fertőzött, de fertőzhető: Ezen kategóriába tartozik a lakosság többsége (kezdetben majdnem mindenki). Az ebben a kategóriában lévő emberek még nem estek át a fertőzésen, de fogékonyak a fertőzésre, azaz potenciálisan fertőzővé válhatnak, ha egy fertőzöttel érintkeznek - ilyenkor a következő állapotba, azaz a lappangó fertőzöttek közé kerülnek.
Lappangási stádiumban lévő fertőzött: Az ezen kategóriába eső embereknél a betegség a lappangási fázisban van. Ilyenkor a betegnek még nincsenek tünetei és még nem fertőz, de néhány napon belül megjelennek az első tünetek, a beteg fertőzővé válik és átkerül az enyhe állapotú fertőzőek közé. Az átmenet átlagos hossza a modell paraméterek között változtatható.
Enyhe állapotú fertőzött: Ebben a kategóriában a beteg már megfertőzhet másokat, de még nem szorul kórházi ellátásra. Innentől kétféle utat követhet a beteg: ha a betegség lefolyása enyhe marad, akkor néhány nap után átkerül a gyógyultak közé, ha viszont súlyosbodik a fertőzés, akkor átkerül a kórházi ellátásra szoruló fertőzöttek közé. Az átmenetig tartó átlagos időtartam hossza, az állapot súlyosbodásának valószínűsége, valamint a beteg által naponta okozott további fertőzések száma a modell paraméterei között változtatható.
Kórházi ápolásra szoruló fertőzött: Ebben a kategóriában a beteg már kórházi kezelés alatt van, és ezzel párhuzamosan lecsökken az általa naponta okozott további fertőzések száma (hiszen a kórházban, sterilebb környezetben, hozzáértő orvosok és nővérek keze alatt kisebb az esélye annak, hogy továbbadja a fertőzést). Innentől ismét kétféle utat követhet a beteg: vagy javul az állapota és néhány nap után átkerül a gyógyultak közé, vagy tovább súlyosbodik az állapota és intenzív ellátásra lesz szüksége. Az átmenetig tartó átlagos időtartam hossza, az állapot további súlyosbodásának valószínűsége, valamint a beteg által napontaokozott további fertőzések száma a modell paraméterei között változtatható.
Intenzív ellátásra szoruló fertőzött: Ebben a kategóriában a beteg már az intenzív osztályon fekszik, és az intenzív osztályon kezelt betegek halálozási arányának megfelelő valószínűséggel lép tovább a gyógyultak vagy az elhalálozottak közé. Az intenzív osztályon kezeltek halálozási aránya, valamint az intenzív osztályon töltött napok átlagos száma a modell paraméterei között változtatható.
Gyógyultak és elhunytak: Ez a két állapot a modell két lehetséges végkimenetele. A gyógyultakról feltételezzük, hogy a fertőzés lefolyása során védettséget szereztek a további fertőzésekkel szemben, így a teljes lakosságban előbb-utóbb kialakul a nyájimmunitás, amikor a meglévő fertőzöttek által naponta okozott további fertőzések száma annyira lecsökken, hogy kisebbé válik, mint az egy nap alatt meggyógyultak száma.

A modell alapfeltételezése, hogy halálozás csak az intenzív osztályos kezelés után következik be, a korábbi stádiumokból vagy meggyógyulni lehet, vagy az eggyel súlyosabb stádiumba lépni.

A modell továbbá azt is feltételezi, hogy a lakosság "jól kevert", azaz a fertőzöttek és a még nem fertőzöttek egyenletes valószínűséggel tudnak kapcsolatba lépni egymással, nincsenek elszigetelt, hatékony és hermetikus karanténba zárt fertőző gócok, amelyek nem tudnak a még nem fertőzöttekkel kapcsolatba lépni. Amennyiben ilyen hatékony karantén-intézkedésekre sor kerül, az ily módon elzárt fertőzöttek számát gyakorlatilag egyben ki lehetne vonni az egy adott napon érvényes fertőzöttek számából.

Az egyes állapotokban töltött idő hossza a modell jellegéből adódóan (egyszerű differenciálegyenletek) exponenciális eloszlást követ, a modell paraméterei között állítható átlagok tehát a mögöttük lévő exponenciális eloszlás átlagát állítják.

Annak érdekében, hogy figyelembe tudjuk venni a vírus terjedésének Magyarországra feltételezett csökkenő trendjét, a modell lehetővé teszi, hogy a fertőzési rátát hetente a kezdeti fertőzési ráta adott százalékával csökkentsük, így véges időn belül elérve az R = 1 állapotot, tehát a járvány csúcsát. Amennyiben ezzel nem szeretnénk számolni, a fertőzési ráta csökkenését 0%-ra kell állítani.

Differenciálegyenletek és technikai részletek

A modell mögött az alábbi differenciálegyenletrendszer van, amelyet a böngésző negyedrendű Runge-Kutta módszerrel old meg a grafikonok rajzolása során:

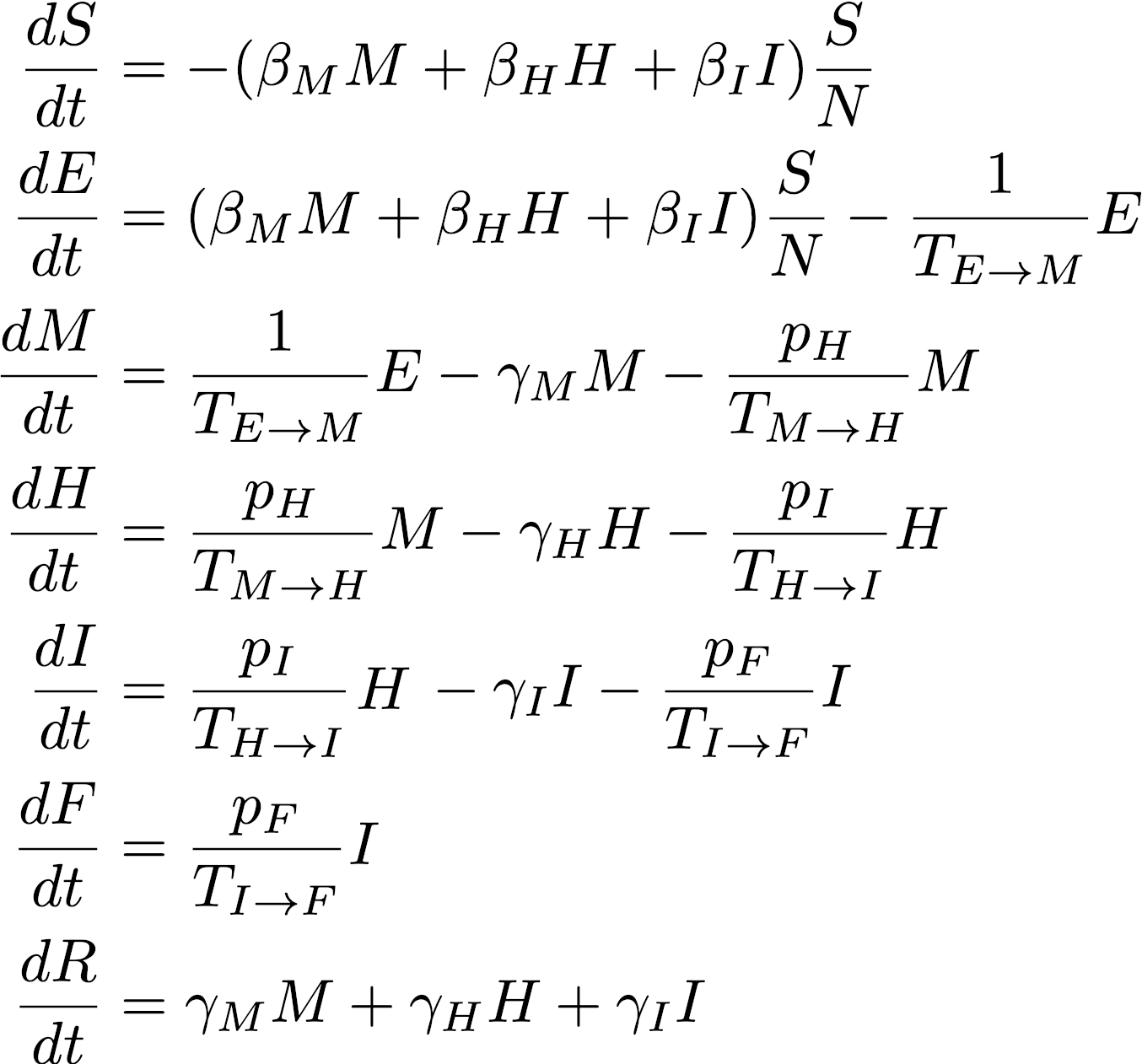
A változók és indexek jelentése:

N - a teljes populáció mérete
S - susceptible, fertőzhető betegek száma
E - exposed, lappangási stádiumban lévő betegek száma
M - mild, enyhe fertőzési stádiumban lévő betegek száma
H - hospitalized, kórházi kezelés alatt lévő betegek száma
I - intensive care, intenzív osztályos kezelés alatt lévő betegek száma
F - fatalities, halálozások száma
R - recovered, gyógyultak száma
β_M, β_H, β_I - az egyes fertőzöttségi szintek fertőzési rátája
γ_M, γ_H, γ_I - az egyes fertőzöttségi szintek gyógyulási rátája
T_E→M, T_M→H, T_H→I, T_I→F - az egyes fertőzöttségi szintek közötti átmenetek időtartamának átlagos hossza
p_H - enyhe stádiumban lévő betegek között a későbbi kórházi kezelésre szorulóak aránya
p_I - kórházi kezelés alatt lévő betegek között a későbbi intenzív ellátásra szorulóak aránya
p_F - halálozási ráta az intenzív ellátásra szoruló betegek között

Paraméterek értékeihez tartozó megfontolások és hivatkozások

Lappangási idő hossza: WHO oldala szerint:"Most estimates of the incubation period for COVID-19 range from 1-14 days, most commonly around five days".
Lauer és mtsai (Ann Intern Med, 2020. március 10.) szerint: "The median incubation period was estimated to be 5.1 days (95% CI, 4.5 to 5.8 days), and 97.5% of those who develop symptoms will do so within 11.5 days (CI, 8.2 to 15.6 days) of infection".
Enyhe szakasz hossza (a kórházba kerülésig): ISARIC Konzorcium COVID-19 jelentése (2020. április 2.) szerint: "The observed mean number of days from (first) symptom onset to hospital admission is 6.9".
Kórházban töltött idő hossza: ISARIC Konzorcium COVID-19 jelentése (2020. április 2.) szerint: "The observed mean duration for the number of days from hospital admission to outcome (death or discharge) is 6.5 days, with a standard deviation (SD) of 5.7".
Intenzív osztályon töltött idő hossza: ISARIC Konzorcium COVID-19 jelentése (2020. április 2.) szerint: "The duration of stay in the ICU has a mean of 6.1 days (SD: 4.9 days) — estimated on only those cases with complete records for ICU duration or ICU start/end dates (N = 87)".
Kórházi kezelésre és intenzív ellátásra szoruló betegek aránya: Ezeket az adatokat az Operatív Törzs napi tájékoztatóiból rögzített hopsitalizációs számokból és a lélegeztetőgépre kötött betegek számából származtatom, 7 napos exponenciális mozgóátlagot számolva és abból az utolsó napi adatot alapul véve. Viszonyítási alapul Ferguson és mtsai (2020. március 16.) tanulmányának 1. táblázatát érdemes még megnézni. A tanulmány életkor szerinti lebontásban közli a kórházi kezelésre szoruló betegek arányának, valamint a közülük intenzív ellátásra szorulóak arányának becslését nagy-britanniai és amerikai kontextusban. Az általuk közölt adatokat a magyarországi korfa 2019-es adatai alapján átsúlyozva 8.2%-os kórházi kezelési és 15.3%-os intenzív ellátási arányt lehetne kapni.
Halálozási arány a kritikus állapotban lévő betegek közül: Szintén Ferguson és mtsai (2020. március 16.) tanulmányának 1. táblázata alapján közvetetten számítható a halálozási arány; Ferguson és mtsai az utolsó oszlopban az összes fertőzésre vetített halálozási arányszámot (infection fatality ratio, IFR) közli, ebből a táblázat további adatai alapján egyszerű osztással-szorzással számítható, hogy az intenzív osztályra kerültek számához képest mi a halálozási arány a kor függvényében. A kapott, 40-50% közötti halálozási arányokat a magyarországi korfa szerint újrasúlyozva adódik a jelen modellben használt 47.1%-os arány. Itt is érdemes megjegyezni, hogy ez az arány magasabb, mint az ISARIC Konzorcium COVID-19 jelentése (2020. április 2.) szerint empirikusan számítható érték: "Of these 251 patients who were admitted into ICU, 51 died, 157 are still in hospital and 26 have recovered and been discharged". 51 / 251 = 20.3%, ez azonban valószínűleg alulbecslés, hiszen azt feltételezi, hogy a 157, még kezelés alatt álló beteg mind meg fog gyógyulni.
Fertőzési ráták: A fertőzési ráták beállításához azzal az alapfeltételezéssel éltem, hogy egy kórházi vagy intenzív kezelés alatt álló beteg fertőzési rátája 20%-a egy kórházi kezelés alatt nem álló fertőzötthöz képest (tehát ha pl egy kórházi kezelés alatt nem álló fertőzött átlagosan naponta 1 további fertőzést okoz, akkor egy kórházi kezelés alatt álló fertőzött csak 0.2-t). Ezek után a fertőzési ráták nagyságrendjét úgy állítottam be, hogy a modell aktuális R reprodukciós rátája megegyezzen azzal az értékkel, amit a hivatalos napi fertőzési adatokból becsülni lehet. Az egyszerűség kedvéért a modell az enyhe fertőzöttek fertőzési rátáját engedi szabadon állítani, de a háttérben a 20%-os feltételezés alapján ehhez igazítja a kórházban lévők és a kritikus esetek fertőzési rátáját is. Ha igény van rá, ezeket a paramétereket külön is beállíthatóvá tudom tenni majd.
Szimuláció kezdeti állapota: A szimuláció kezdeti állapotát a mai napon ismert hivatalos statisztikák alapján állítottam be. Mivel a lappangók száma nem ismert, de minden bizonnyal nagyságrendileg legalább akkora, mint a fertőzöttek száma, ezért kezdetben a lappangók és fertőzöttek számát ugyanakkorára vettem. A modell egyébként nem különösebben érzékeny a lappangók és a fertőzöttek kezdeti arányára.